If you want to see more math behind a Fourier Transform, read my DFT notes.

Fast Fourier Transform

The DFT is a slow algorithm, over time much faster alternatives have been developed. One of the most popular is the Radix-2 Fast Fourier Transform which was developed in 1965 by Tukey and Cooley. It comes in two flavours - decimation in frequency, and decimation in time. I'll only deal with the latter.

The basic premise behind the Radix-2 Decimation in Time algorithm is that if we define an N-element FFT as:

$FFT_N\left(k,f\right) & = & \sum^{N-1}_{n=0}f\left(n\right)e^{-i2\pi kn\!/N}$

Then we can express one FFT of N inputs as two FFTs of N/2 inputs:

$FFT_N \left(k,f\right) & = & \sum^{N\!/2-1}_{n=0}f\left(2n\right) e^{-i2\pi k\left(2n\right)/N} + \sum^{N\!/2-1}_{n=0}f\left(2n+1\right) e^{-i2\pi k\left(2n+1\right)/N}\\ FFT_N \left(k,f\right) & = & \sum^{N\!/2-1}_{n=0}f\left(2n\right) e^{-i2\pi kn\!/\left(N\!/2\right)} + e^{-i2\pi k\!/N} \sum^{N\!/2-1}_{n=0}f\left(2n+1\right) e^{-i2\pi kn\!/\left(N\!/2\right)}$

The sub-transforms will only give us values for k between zero and N/2. The other half of the values are found by using the periodicity of the Fourier Transform: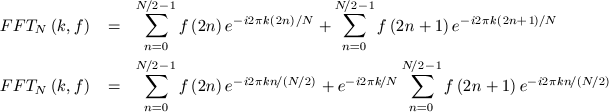

$FFT_{N\!/2}\left(k+N\!/2,f\right) & = & FFT_{N\!/2}\left(k,f\right)$

It looks a little neater if we split f into even and odd elements: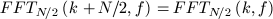

$FFT_N\left(k,f\right) = FFT_{N\!/2}\left(k,f_e\right) + e^{-i2\pi k\!/N} FFT_{N\!/2}\left(k,f_o\right)\\ FFT_N\left(k+N\!/2,f\right) = FFT_{N\!/2}\left(k,f_e\right) - e^{-i2\pi k\!/N} FFT_{N\!/2}\left(k,f_o\right)\\ \textrm{where } f_e\left(n\right) = f\left(2n\right)\\ \textrm{and } f_o\left(n\right) = f\left(2n+1\right)$

We can express each one of those N/2-input FFTs as a sum of two N/4-input FFTs and so forth. As long as N is a power of two, we can keep splitting the FFT down until we get to a whole heap of 1-element transforms.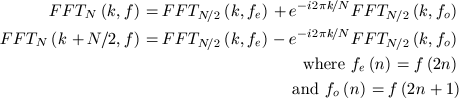

[fft1.c] My first attempt at implementing this was much faster than the DFT but very slow for an FFT because it was recursive and allocated memory dynamically to split f into evens and odds. (Because I wanted to see the math work before I launched into an even slightly complicated implementation)

[fft2.c] My second attempt - I sort the inputs into a bit-reversed order and then use a recursive, in-place FFT. No malloc abuse happens.

[fft3.c] My third attempt - eliminated recursion. There's still plenty of space for optimisation (such as taking advantage of trivial twiddle factors in the first few passes) but this is where I'm calling it quits.

Faster Fourier Transforms

If you're looking for a really fast FFT implementation, try one of these:

Fourier's Last Transform

rp: The process that transformed Fourier back to the elements of which he was composed.