Rotation

First written in 2006.
Last updated 2014-06-29.

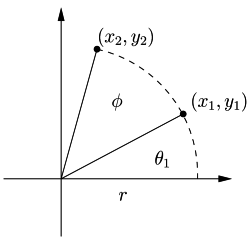
Rotate a point, $(x_1, y_1)$, around the origin, by the angle $\phi$, resulting in a new point, $(x_2, y_2)$:

$$ \begin{eqnarray*} x_2 & = & x_1 \cos \phi - y_1 \sin \phi\\ y_2 & = & y_1 \cos \phi + x_1 \sin \phi \end{eqnarray*} $$

How to derive the rotation formulas

Start with a point: $$p_1 = (x_1, y_1)$$

In polar coordinates, this is: $$ \begin{eqnarray*} x_1 = r \cos \theta_1\\ y_1 = r \sin \theta_1 \end{eqnarray*} $$

The rotated point will be: $$ \begin{eqnarray*} x_2 & = & r \cos \left(\theta_1 + \phi\right) \\ y_2 & = & r \sin \left(\theta_1 + \phi\right) \end{eqnarray*} $$

Remember the trigonometric identities for addition of angles: (we'll get to these later) $$ \begin{eqnarray*} \sin \left(a + b\right) & = & \sin a \cos b + \cos a \sin b \\ \cos \left(a + b\right) & = & \cos a \cos b - \sin a \sin b \end{eqnarray*} $$

Substituting these in, we get: $$ \begin{eqnarray*} x_2 & = & r \cos \left(\theta_1 + \phi\right) \\ x_2 & = & r \left( \cos \theta_1 \cos \phi - \sin \theta_1 \sin \phi \right) \end{eqnarray*} $$

Using the equations for $x_1$ and $y_1$, we can simplify this: $$ \begin{eqnarray*} x_2 & = & \left( r \cos \theta_1 \right) \cos \phi - \left( r \sin \theta_1 \right) \sin \phi\\ x_2 & = & x_1 \cos \phi - y_1 \sin \phi \end{eqnarray*} $$

Likewise, for $y_2$: $$ \begin{eqnarray*} y_2 & = & r \sin \left(\theta_1 + \phi\right) \\ y_2 & = & r \left( \sin \theta_1 \cos \phi + \cos \theta_1 \sin \phi \right) \\ y_2 & = & y_1 \cos \phi + x_1 \sin \phi \end{eqnarray*} $$

How to derive the addition-of-angles formulas

A complex number on the unit circle, in exponential form: $$e^{\theta i} = \cos \theta + i \sin \theta$$

Multiplying two such complex numbers: $$e^{ai} \times e^{bi} = e^{\left(a+b\right)i}$$

So: $$ \begin{eqnarray*} e^{\left(a+b\right)i} & = & \cos\left(a+b\right) + i \sin\left(a+b\right) \\ e^{ai} \times e^{bi} & = & \left(\cos a + i \sin a\right) \times\\ & & \left(\cos b + i \sin b\right)\\ & = & \cos a \cos b + i \cos a \sin b +\\ & & i \sin a \cos b - \sin a \sin b\\ \end{eqnarray*} $$

Separating the real and complex components: $$ \begin{eqnarray*} \cos\left(a+b\right) & = & \cos a \cos b - \sin a \sin b\\ \sin\left(a+b\right) & = & \cos a \sin b + \sin a \cos b \end{eqnarray*} $$

Implementation and optimization

Here's a straightforward implementation of rotation in C++:

void rot1(const double x1, const double y1, const double theta,
          double* x2, double* y2) {
  const double s = sin(theta);
  const double c = cos(theta);
  *x2 = x1 * c - y1 * s;
  *y2 = y1 * c + x1 * s;
}

The above costs 4 multiplies, 1 add, 1 subtract.

We can trade one of the multiplies for 2 adds and 1 subtract:

void rot2(const double x1, const double y1, const double theta,
          double* x2, double* y2) {
  const double s = sin(theta);
  const double c = cos(theta);
  const double z = x1 * (s + c);
  *x2 = z - (x1 + y1) * s;
  *y2 = z + (y1 - x1) * c;
}

The above costs 3 multiplies, 3 adds, 2 subtracts.

If the angle is fixed, there's a further optimization possible:

void rot3(const double x1, const double y1,
          double* x2, double* y2) {
  const double s = sin(1. * M_PI / 16.);
  const double c = cos(1. * M_PI / 16.);
  const double z = c * (x1 + y1);
  *x2 = (-s-c) * y1 + z;
  *y2 = ( s-c) * x1 + z;
}

The above costs 3 multiplies and 3 adds, because -s-c and s-c are turned into constants.

All the code is here: rot.cc

I'm not counting operations by looking at the C++ code, but by looking at the generated assembler. There are instructions and results in the file.